记录灵感、技术、思考

JavaScript编程之乱序洗牌(shuffle)

•

Math.random

一个网上常见的方法是 Math.random():


var values = [1,2,3,4,5];

values.sort(function() {
    return Math.random() -0.5
})

console.log(values)

Math.random()-0.5 随机得到一个正数、复数或者0.如果是正数则降序排列，如果是复数则升序排列，0就是不便。然后不断的升序、降序最后获得一个乱序的数组。

看似没问题，实际上却有问题。

设计一个测试的demo，测试原理是：将 [1, 2, 3, 4, 5] 乱序 10 万次，计算乱序后的数组的最后一个元素是 1、2、3、4、5 的次数分别是多少。

var times = [0, 0, 0, 0, 0];

for (var i = 0; i < 100000; i++) {
    
    let arr = [1, 2, 3, 4, 5];
    
    arr.sort(() => Math.random() - 0.5);
    
    times[arr[4]-1]++;

}

console.log(times)

实测结果

➜  browser-test node shuffle.js 
[ 6190, 6248, 12630, 25052, 49880 ]
➜  browser-test node shuffle.js
[ 6325, 6315, 12548, 24866, 49946 ]
➜  browser-test node shuffle.js
[ 6194, 6316, 12643, 24898, 49949 ]
➜  browser-test node shuffle.js
[ 6391, 6286, 12473, 24825, 50025 ]
➜  browser-test node shuffle.js
[ 6490, 6179, 12602, 24991, 49738 ]
➜  browser-test node shuffle.js
[ 6331, 6369, 12516, 24888, 49896 ]

可以看到 1、2、3、4、5 他们的比例并不是均匀，这是为什么呢？

插入排序

想了解这个还需要先从sort开始，ECMA之规定了效果，没有规定时限方式。Chrome的V8为例，V8的sort，当目标数组长度小于10，使用插入排序，反之使用快速排序和插入排序的混合排序。

备注：

插入排序的算法


function InsertionSort(a, from, to) {
    for (var i = from + 1; i < to; i++) {
        var element = a[i];
        for (var j = i - 1; j >= from; j--) {
            var tmp = a[j];
            var order = comparefn(tmp, element);
            if (order > 0) {
                a[j + 1] = tmp;
            } else {
                break;
            }
        }
        a[j + 1] = element;
    }
};

其原理在于将第一个元素视为有序序列，遍历数组，将之后的元素依次插入这个构建的有序序列中。

我们来个简单的示意图：

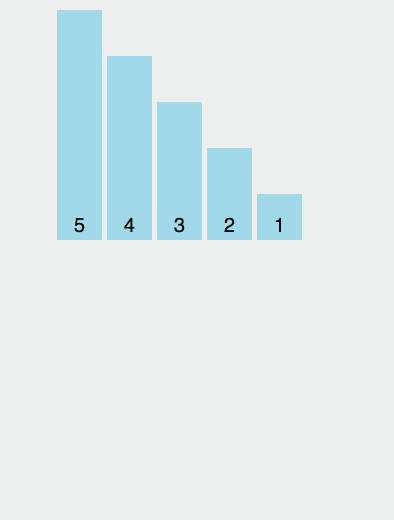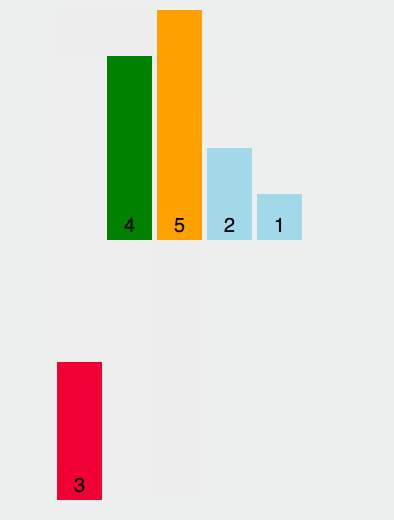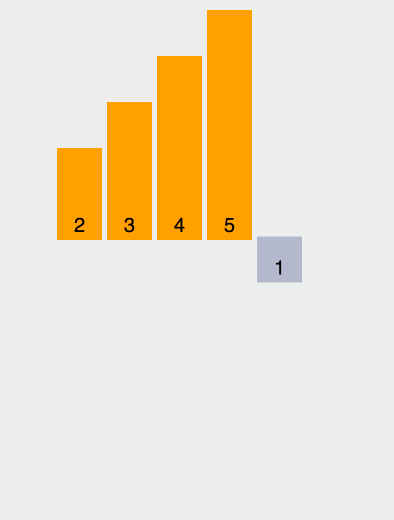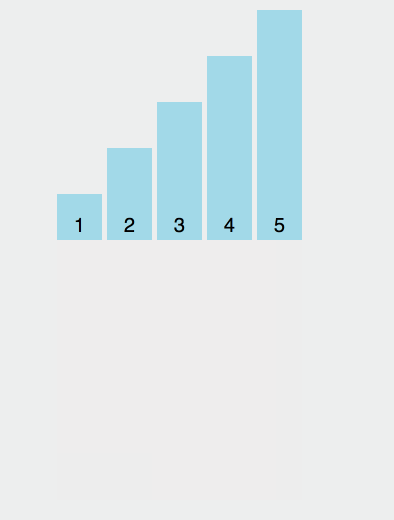
insertion_sort.gif

具体分析

明白了插入排序的原理，我们来具体分析下 [1, 2, 3] 这个数组乱序的结果。

演示代码为：

var values = [1, 2, 3];

values.sort(function(){
    return Math.random() - 0.5;
});

此时的sort地层使用的是插入排序，insertion sort函数的from 0，to 是3

逐步分析

因为插入排序视第一个元素为有序，所以数组的外层循环从i=1开始，a[i] 值为2，此时内层循环遍历,比较 compare(1,2),因为Math.random()-0.5 的结果有50% 概率小于0.有 50%的概率对于0。 所以 50%概率性 [2,1,3], 50%概率是 [1,2,3]

假设依然是 [1,2,3] 再进行一次分析，接着遍历 i=2. a[i] = 3，此时内层循环遍历比较 compare(2，3)

50%概率不便，然后遍历结束。 50%概率辩才 [1,3,2],因为还没有找到3的正确位置，所以还是会进行遍历，所以在这的50%又会进行一次比较 compare(1,3) 然后 50%的概率不变，数组为 [1,3,2] 遍历结束，50%的概率发生变化[3,1,2]。

把所有情况总结为一个表格

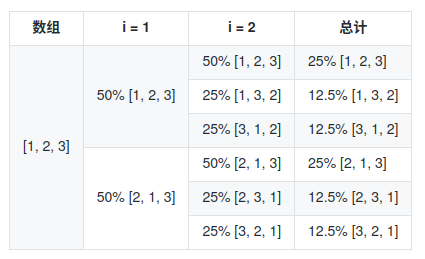
insert_sort_analysis.png

接下来来验证下这个推论

var times = 100000;
var res = {};

for (var i = 0; i < times; i++) {
    
    var arr = [1, 2, 3];
    arr.sort(() => Math.random() - 0.5);
    
    var key = JSON.stringify(arr);
    res[key] ? res[key]++ :  res[key] = 1;
}

// 为了方便展示，转换成百分比
for (var key in res) {
    res[key] = res[key] / times * 100 + '%'
}

console.log(res)

输出结果

➜  browser-test node shuffle.js
{ '[2,1,3]': '25.291000000000004%',
  '[3,2,1]': '12.284%',
  '[3,1,2]': '12.592999999999998%',
  '[1,2,3]': '24.978%',
  '[1,3,2]': '12.431000000000001%',
  '[2,3,1]': '12.423%' }

总结

sort无法做到真正的排序根本原因在于什么呢？其实就在于在插入排序的算法中，当待排序元素跟有序元素进行比较时，一旦确定了位置，就不会再跟位置前面的有序元素进行比较，所以就乱序的不彻底。

Fisher–Yates 算法

function shuffle(a) {
    var j, x, i;
    for (i = a.length; i; i--) {
        j = Math.floor(Math.random() * i);
        x = a[i - 1];
        a[i - 1] = a[j];
        a[j] = x;
    }
    return a;
}

// es6

function shuffle(a) {
    for (let i = a.length; i; i--) {
        let j = Math.floor(Math.random() * i);
        [a[i - 1], a[j]] = [a[j], a[i - 1]];
    }
    return a;
}

原理很简单，就是遍历数组元素，然后将当前元素与以后随机位置的元素进行交换，从代码中也可以看出，这样乱序的就会更加彻底。

var times = 100000;
var res = {};

for (var i = 0; i < times; i++) {
    var arr = shuffle([1, 2, 3]);

    var key = JSON.stringify(arr);
    res[key] ? res[key]++ :  res[key] = 1;
}

// 为了方便展示，转换成百分比
for (var key in res) {
    res[key] = res[key] / times * 100 + '%'
}

console.log(res)

测试结果

➜  browser-test node shuffle.js
{ '[3,2,1]': '16.607%',
  '[1,2,3]': '16.589000000000002%',
  '[2,3,1]': '16.726%',
  '[3,1,2]': '16.756999999999998%',
  '[1,3,2]': '16.564%',
  '[2,1,3]': '16.756999999999998%' }

参考

Mark24

Everything can Mix.